花弁が語るフィボナッチの秘密

　息子が"母の日"にアレンジメントフラワーを持ってきた。妻は思わぬ贈り物に驚き、この日を覚えていてくれたことがよほど嬉しかったようだ。「この花の名前は何だろう」、「こんな花、見たことがない」など、日頃聞かない言葉が部屋を華やかにしていった。

　私が「花弁がたくさんある花は豪華に見えるなあ」と何気なく話すと、「この花の花弁は何枚あるのかなあ」と妻が呟いた。

数日後、花は早く弱ってきた。そうこうしているうちに、私はあの妻の一言に引きずられていたのか、花弁の枚数に興味が移っていった。花弁を一枚ずつ剥がしてはテーブルに並べ、一つの花に何枚あるのか数えながら、頭の中では"フィボナッチ数列"が渦巻いていた。

　フィボナッチ数列とは、1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...と続く数列で、前の二つの数を足すと次の数になるという、いたって簡単な前提から成り立っている。

　花の名前が分からないので、A・B・C・・・・として花弁の枚数を調べてみた。5枚、21枚、34枚はフィボナッチ数列通りだったが、13枚と55枚は1枚違いの微妙なずれがあった。花弁の枚数が89枚と多くなると75枚となり、かなりのずれが生じていた。花弁の数が多くなるほど、成長のプロセスが複雑になり、ずれが生じてくるのだろう。

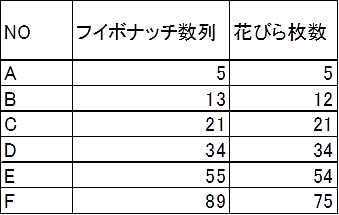
　それにしても、花弁の枚数が概ねこの数列に一致していることに驚かされた。単純な「加算」ではなく、常に「隣り合ったもの」との相互作用の中で、次の「新たなもの」が最適な形で生まれてくる成長プロセスが繰り広げられていると思われた。自然界は、前の二つの数を足すと次の数になるという、馬鹿馬鹿しいほど簡明なカラクリから成り立っているのだ。

　では、なぜこれほど花弁の枚数がフィボナッチ数列に一致するのか。これには隠れた秘密があった。それは黄金比である。

黄金比とは、自然界において人間にとって最も美しく安定して見える比率のことで、古代ギリシャ時代から建築や芸術に使用されてきた。フィボナッチ数列の隣接する項の比は、項数が大きくなるにつれて黄金比（約1.618）に収束する。

　ここが核心なのだが、この黄金比によって、植物の成長点では最も効率的な角度で花弁が配置されるように進化していくのである。黄金比から導かれる最適角度が約137.5度（黄金角）で、螺旋状に花弁が配置される。すると、最も密度が高く効率的な配置が実現される。結果として、花弁数は自然にフィボナッチ数になっているのである。

　分かりやすく言うと、花弁数がフィボナッチ数列になることで、未来につなげる種子が最密充填状態になっているのだ。

　フィボナッチは約800年前、イタリアのピサで生まれた数学者で、インド・アラビア数字の10進法をヨーロッパに伝えた人物であった。彼は「面白い数列」を見出しただけで、この数列が黄金比に収束することは知らなかったと推測される。17世紀にケプラーがフィボナッチ数列と黄金比の関係を指摘し、19世紀後半になって花弁配置との関係に注目されるようになった。現代ではコンピュータシミュレーションで最密充填理論が確立されている。

フィボナッチの「面白い数列」の発見から、その深遠な幾何学的意味や自然界での普遍性の解明まで、一人の天才の出現というより、累積的な知識の発展の産物だったのである。

　ただし、自然界はこんな単純な法則だけで言い尽くせるものでもない。フィボナッチ数列に従う5枚花弁が最も多く見かけるが、次に見かけるのが4枚の花弁で、これはフィボナッチ数列ではない。この種の花は、最密充填の構造を必要としないのだろう。 妻の何気ない一言から始まった花弁の観察が、自然界の神秘的な数学的秩序へと導いてくれた。母の日の贈り物は、思わぬ学びの扉を開いてくれたのである。